Préparation des données et calculs initiaux

Désignons par xxx le nom de la structure à résoudre. L'utilisateur doit fournir un fichier xxx.hkl contenant l'ensemble des {h, k, l,  , s(F_H)} observés. Pour la normalisation il est conseillé d'utiliser les programmes de R.Blessing (levy, eval et snbref) ^[1] dont les sources sont disponibles par ftp anonyme à ftp://www.hwi.buffalo.edu/pub/Blessing/Drear (la distribution de SnB v2.0 inclut ces programmes). Les facteurs de structure normalisés sont rangés dans le fichier xxx.ref (figure 3).

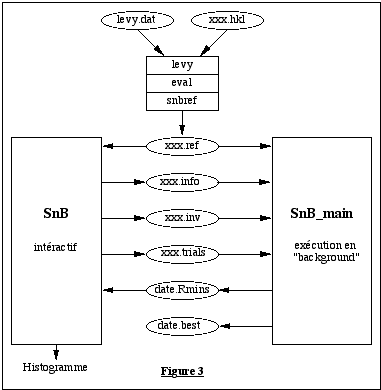
Le logiciel est en fait composé de deux programmes.

Le programme intéractif SnB écrit en langage C (+ Java pour SnB v2.0) sert à entrer les données critallographiques et à choisir les options désirées. Il range ces informations dans le fichier xxx.info. Puis SnB effectue un certain nombre d'initialisations, comme le calcul des invariants stoqués dans le fichier xxx.inv, et la génération des modèles de structures aléatoires initiaux dans xxx.trials.

Options à utiliser

Les options recommandées par les auteurs de SnB suivant les types de structures sont indiquées ci-dessous. Ce sont les options par défaut de SnB v2.0, mais si on utilise la version 1.5 on devra vérifier les options proposées et les modifier éventuellement (passer en mode " expert " si nécessaire).

Affinement des phases : méthode " Parameter Shift "
Groupes d'espace non centro-symétriques :

Incrément de phase Df : 90°
Nombre maximum de modifications par phase : 2
Nombre de passes : 3 (ou 1 pour P1)

Incrément de phase Df : 180°
Nombre maximum de modifications par phase : 1
Nombre de passes : 1

Nombre de phases : 10n
Nombre de triplets : 100n
Nombre de quadruplets : 0
Nombre de cycles SnB :

n/2 si n < 400 et des atomes plus lourds que O sont présents
sinon n

0.4n si des atomes plus lourds que O sont présents
sinon 0.8n

Augmenter le nombre d'invariants : 200n à 500n
Faire plus de cycles SnB : entre n et 1.5n
La présence d'atomes " lourds " (Cl ou S) augmente la probabilité de succès

Histogramme résultat

La résolution proprement dite est effectuée par un deuxième programme SnB_main écrit en Fortran, et qui est lancé par SnB (spawn) lorsque l'utilisateur décide de commencer le calcul (figure 3). SnB_main s'exécute en " background " et communique avec SnB via des fichiers. En particulier à la fin du traitement de chaque modèle il écrit dans le fichier date.Rmins la valeur finale de la fonction minimum. De plus il maintient à jour le ficher date.best qui contient la meilleure structure obtenue, c'est-à-dire celle correspondant à la plus petite valeur de R(f).

A tout moment pendant que le calcul se déroule, ce qui peut durer plusieurs jours ou même plusieures semaines, l'utilisateur a la possibilité de visualiser à l'aide de SnB l'histogramme des valeurs de la fonction minimum pour les modèles déjà traités :

- si cet histogramme est de type Gaussien, c'est-à-dire avec toutes les valeurs de R(f) regroupées en une seule bosse, c'est qu'aucune solution n'a été trouvée.

- au contraire si une ou quelques valeurs de R(f) se détachent assez nettement des autres, du côté des valeurs inférieures, c'est qu'elles correspondent à des solutions. Un exemple ayant donné trois solutions est présenté figure 4.

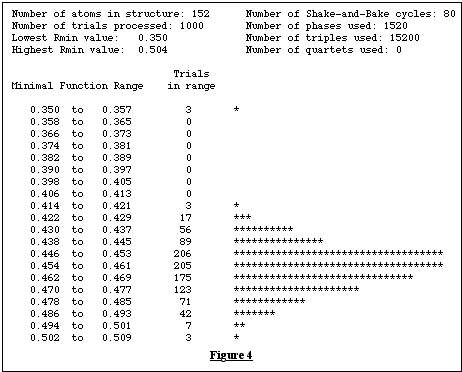
Le fichier date.best contient alors la meilleure solution. Celle-ci est généralement assez grossière ou incomplète ; elle peut être améliorée avec SnB en effectuant des cycles supplémentaires avec différentes options, mais notre expérience nous a montré qu'il était plus rapide de rentrer la solution sous forme de fragment dans un programme traditionnel, pour la terminer puis l'affiner.

4 - Exemples d'applications :