La fonction minimum ^[5]

On considère une structure comportant N atomes en positions inconnues  dans la maille, pour laquelle la mesure des intensités de diffraction X d'un ensemble de réflexions {H} a fournit après normalisation les modules des facteurs de structure  .

Si on suppose que les atomes ont tous à peu près le même poids, les facteurs de structure normalisés s'écrivent sous la forme simplifiée :

On note  les triplets de phases invariants dans un changement d'origine, et  les quadruplets de phases invariants :

D'un point de vue statistique, si on considère les vecteurs position  comme des variables aléatoires indépendantes et uniformément distribuées, les invariants seront aussi des variables aléatoires. Pour un couple de réflexions H, K donné, on peut alors montrer que le cosinus du triplet de phase correspondant  peut être estimé par :

où  et I₀, I₁ sont les fonctions de Bessel modifiées d'ordre 0 et 1 respectivement ; cette estimation sera d'autant plus valide que  sera grand.

De manière identique, pour des réflexions L, M et N données, le cosinus du quadruplet  peut être estimé par :

avec  .

D'où le choix de la fonction minimum utilisée par SnB :

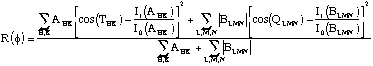
La double somme porte sur les vecteurs du réseau réciproque H, K associés aux triplets  correspondants aux plus grandes valeurs de  et la triple somme sur les vecteurs L, M, N associés aux quadruplets  négatifs. Dans ces sommes,  représente le poids du triplet  et  le poids du quadruplet  .

Le " principe minimum " ^[2,5]

D'après son expression, on constate que R(f) est une mesure de la différence quadratique moyenne entre les cosinus des invariants calculés et leurs valeurs attendues. Le " principe minimum " énoncé par H.Hauptman stipule que :

- pour un nombre suffisant de phases, contraintes à prendre des valeurs consistantes avec une structure atomique, R(f) présente un minimum global lorsque toutes ces phases sont égales à leur vraie valeur.

- lorsque les phases sont égales à leur vraie valeur, R(f) = R_T < 1/2, indépendemment du choix de l'origine et de l'énantiomorphe.

- au contraire pour des phases aléatoires on a R(f) = R_R > 1/2.

Algorithme de SnB ^[6,13]

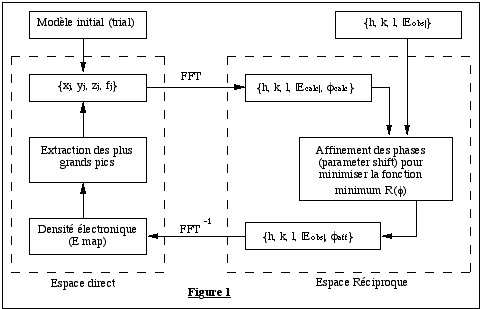
Le fonctionnement de SnB découle directement du principe minimum : il consiste à faire varier les phases dans l'espace réciproque en vue de minimiser la valeur de la fonction minimum, puis à revenir dans l'espace direct pour contraindre les phases à prendre des valeurs consistantes avec une structure atomique. Un nombre (proportionnel à la taille de la structure) de tels cycles est effectué pour tenter de converger vers la solution.

L'algorithme correspondant, schématisé sur la figure 1, comporte donc les étapes suivantes :

- Un modèle initial composé d'un nombre d'atomes inférieur ou égal au nombre recherché est généré ; ces atomes sont placés aléatoirement dans l'unité asymétrique avec la contrainte qu'ils doivent être distants d'au moins 1.2 Å, et ne pas être liés à plus de quatre voisins.

- Un calcul des facteurs de structure normalisés est effectué pour le modèle courant, et les phases ainsi obtenues seront affectées aux  observés.

- L'affinement des phases peut être réalisé par diverses méthodes, dont la traditionelle formule de la tangente ^[11], mais il est recommandé d'utiliser celle par défaut, dite " parameter shift ". Les phases sont considérées par ordre décroissant des valeurs de  associées ; lors de la modification de la i^ème phase, la fonction minimum est évaluée pour sa valeur actuelle f_i, pour f_i + Df et pourf_i - Df, où Df est un incrément fixé (Figure 2). Si R(f) est minimum pour la valeur actuelle de f_i celle-ci est conservée et on passe à la phase suivante f_i+1 . Sinon on choisit le sens de variation donnant R(f) minimum (+Df sur la figure 2) ; la valeur retenue de la phase subit de nouveaux déplacements dans le même sens tant que R(f) diminue et qu'un nombre maximum de déplacements n'a pas été dépassé (3 dans l'exemple).

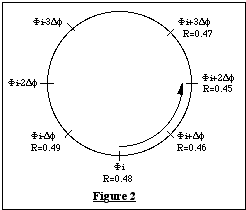
Par exemple sur la figure 2, la nouvelle valeur de f_i sera f_i + 2 Df. On notera que cette nouvelle valeur remplace immédiatement l'ancienne en mémoire, et est donc utilisée lors de l'affinement des phases suivantes. Lorsque le programme a parcouru toutes les phases, il recommence ce processus d'affinement un certain nombre de fois (3 par défaut).

- A l'aide des  observés et des phases affinées, SnB calcule une densité électronique par transformée de Fourier inverse, retournant ainsi dans l'espace direct (figure 1).

- Le programme extrait ensuite les plus grands pics de la densité électronique, et ces pics sont considérés comme des atomes. Ils remplacent le modèle initial, et seront utilisés pour le calcul des facteurs de stucture lors du cycle suivant. Dans le cas où la structure possède des atomes " lourds " (par exemples des S) un nombre correspondant des plus grands pics extraits sera affecté du facteur de diffusion atomique f adéquat.

3 - Utilisation pratique de SnB :