Authors:
A. Altomare, G. Cascarano, C. Giacovazzo, A. Guagliardi, A.G.G. Moliterni,
Istituto di Ricerca per lo Sviluppo di Metodologie Cristallografiche, CNR,
c/o Dipartimento Geomineralogico, Campus Universitario, Via Orabona 4, 70125 Bari, Italy.
M.C. Burla, G. Polidori
Dipartimento di Scienze della Terra, Piazza Universita', 06100 Perugia, Italy.
M. Camalli, R. Spagna
Istituto di Strutturistica Chimica `G. Giacomello', CNR,
C.P. 10 - Monterotondo stazione - 00016 Roma, Italy.
U S E R' S M A N U A L
Support : sirware@area.ba.cnr.it
Web site : http ://www.ba.cnr.it/IRMEC/SirWare.html
The representation theory, proposed by Giacovazzo (1977,1980) allowed the derivation of powerful methods for estimating structure invariants (s.i.) and structure seminvariants (s.s.). The mathematical approach makes full use of the space group symmetry. SIR uses symmetry in a quite general way allowing the estimation and use of s.i. and s.s. in all the space groups.
The range of options available to experienced crystallographers for choosing their own way of solving crystal structures is rather wide. However scientists untrained in direct methods or experienced people trustful in the SIR default mode often can solve crystal structures without personal intervention.
The setting up of the SIR program was initiated a few years ago. The present version (SIR97) of the program is the fourth release which we consider suitable for distribution and includes several new features with respect to the previous version, SIR92 (Altomare, Cascarano, Giacovazzo, Guagliardi, Burla, Polidori, Camalli (1994)). A major feature is represented by the integration of the direct method section with that devoted to the crystal structure refinement [ the evolution of CAOS (Crystallographic Analysis Operating System, 1986)].
Depending on the refinement program available the user can fix the default format for the output peak file by modifying the variable jout.
The default dimensions of the graphic window are stored in the variables kscrx and kscry (720x525).The user can only increase these values depending on screen resolution.
The default use of the graphic window is determined by the value of the variable kscreen.
If kscreen is set to zero the window will not be displayed unless the %WINDOW command is used.
To be able to implement the graphic part the user has to compile the FORTRAN files and one C-file and then link together using the library of X-Window. Examples of Makefile are supplied with program files.
If a graphic device is not available then remove all C files and rename the file xmr97.txt as :
xmr97.f for Risc/6000, HP
xmr97sgi.f for Silicon Graphics, SUN, Linux, Digital Alpha (Unix)
xmr97vms.f for Digital VMS
and then compile and link.
- tar xvf sir97.tar
- uncompress *.Z
- copy the files SirWare.* in your HOME directory
- create the executable file using the command
make -f file_name
where file_name must be one of the following:
makefile.aix for Risc/6000
makefile.hp for HP
makefile.sgi for Silicon Graphics
makefile.sun for SUN
makefile.linux for Linux
makefile.axp for Digital Alpha (Unix)
- run the test :
sir97 loganin
- WARNING : the first time the program will take some minutes to create the configuration file SirWare.cfg@Local ; if errors occur or you are not satisfied of the fonts used by the program you have to create the SirWare.cfg@Local :
- edit the file sirware.cfg.all and extract the part you are interested in ; call it
SirWare.cfg@Local ( upper and lower case are mandatory )
- copy the file SirWare.cfg@Local in your HOME directory
- copy the file SirWare.cfg@Local in your HOME directory
- run the test
sir97 loganin
- create the executable file using the command
@build_sir97
- edit the file RUN_SIR97.COM in order to customize it (follow hints in the file) ;
- define in your LOGIN.COM file a symbol, i.e. :
SIR97 == "@DKA100 :[USER.SIR97]RUN_SIR97" ;
- run the test :
sir97 loganin
- WARNING : the first time the program will take some minutes to create the configuration file SirWare.cfg; if errors occur or you are not satisfied of the fonts used by the program you have to create the SirWare.cfg:
- edit the file sirware.cfg.all and extract the part you are interested in ; call it
SirWare.cfg
- copy the files SirWare.cfg in your default directory ( sys$login )
- run the test :
sir97 loganin
- unzip SIR97.ZIP
- install Sir97 on your DeskTop using the standard link mechanism of Windows '95 or NT
- to run the program click on Sir97 icon
SIR97, LIST, DATA, NORMAL, SEMINVARIANTS, INVARIANTS, PHASE, FOURIER/LEAST-SQUARES, MENU, PATTERSON, LSQ, GEOM.
Diffraction data are checked in order to find out equivalent reflections or systematically absent reflections (which are then excluded from the data set) and, eventually, reflections (weak) not included in the data set (Cascarano, Giacovazzo & Guagliardi, 1991).
When some additional prior information, besides positivity and atomicity of electron density, is available, then a suitable renormalization of structure factors is made.
SIR97 is able to deal with the following types of prior information:
a) pseudotranslational symmetry, identified by normalization routine or other source;
b) a well oriented and well positioned molecular fragment (Camalli, Giacovazzo & Spagna,1985; Burla, Cascarano, Fares, Giacovazzo, Polidori & Spagna,1989).
One-phase s.s. are estimated by means of their first and second representation as described by Giacovazzo (1978), Cascarano, Giacovazzo, Calabrese, Burla, Nunzi, Polidori & Viterbo (1984). As a default the second representation is calculated.
Two-phase s.s. are estimated by means of their first representation as described by Giacovazzo, Spagna, Vickovic & Viterbo (1979) and by Burla, Giacovazzo & Polidori (1989).
The estimated s.s. are stored in the direct access file; those evaluated with highest reliability will be actively used in the phasing process while the others will contribute to compute, with other phase relationships, the figure of merit CPHASE.
Negative quartets are generated by combining the psizero triplets in pairs, and those with cross-magnitudes smaller than a given threshold are estimated by means of their first representation, as described by Giacovazzo (1976). These quartets are be actively used in the phasing process (Giacovazzo, Burla & Cascarano, 1992) and will provide an important contribution to the FOM CPHASE.
Active triplets may be estimated according to Cochran's (1955) P3 distribution: the concentration parameter of the von Mises distribution is then
C = 2 * Eh * Ek * Eh-k / N (1)
Triplets can also be estimated according to their second representation (i.e. P10 formula, as described by Cascarano, Giacovazzo, Camalli, Spagna, Burla, Nunzi and Polidori, 1984). The concentration parameter of the new von Mises (i.e. of the same form of Cochran's) distribution is given by
G = C (1 + q) (2)
where q is a function (positive or negative) of all the magnitudes in the second representation of the triplet. The G values are rescaled on the C values and the triplets are ranked in decreasing order of G. The top relationships represent a better selection of triplets with phase value close to zero than that obtained when ranking according to C. These triplets will be actively used in the phase determination process.
Triplets estimated with a negative G represent a sufficiently good selection of relationships close to 180 degrees to be used both for active use in the phasing process (Giacovazzo, Burla & Cascarano, 1992) and for the calculation of a powerful FOM (CPHASE). Triplets with G close to zero are expected to have values widely dispersed around 90 or 270 degrees and are used to compute an enantiomorph sensitive FOM. A similar FOM is also computed using quartets estimated with a very small concentration parameter.
As a default, triplets are estimated according to P10 formula.
The parameter C of the Cochran distribution (say P3) is suitably modified when prior information, such as that described above in the section `NORMAL module', is available. Then triplet phases are no longer expected to be around zero (see quoted references) and may lie anywhere between 0 and 2.
Each relationship is used with its proper weight: the concentration parameter of the first representation for quartets and two-phase s.s., and C or G for triplets.
- CONVERGENCE/DIVERGENCE PROCEDURE -
The convergence procedure (Germain, Main & Woolfson, 1970) is a convenient way of defining an optimum starting set of phases to be expanded by the tangent formula or by any other algorithm.
When the P10 formula is used, as a default, a special convergence process is devised which chooses the starting set according to
![]() (3)
(3)
as suggested by Giacovazzo (1979) and by Burla, Cascarano, Giacovazzo, Nunzi & Polidori (1987), with
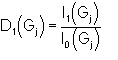
I1 and I0 represent modified Bessel functions of order one and zero respectively. The summation in (3) is over all relationships defining the reflection h. If P3 formula is used the default choice is
![]() (4)
(4)
Once the starting set has been defined, a good pathway for phase expansion is determined by a divergence procedure. In the divergence map, starting from the reflections in the starting set, each new reflection is linked to the preceding ones with the highest value of < >.
- PHASE EXTENSION AND REFINEMENT -
The starting set defined by the preceding step is usually formed by the origin (and enantiomorph) fixing reflections, a few one phase s.s. and a number of other phases which may be obtained:
a) by magic integer permutation (White & Woolfson,1975; Main, 1978),
b) by a random approach (Baggio, Woolfson, Declercq & Germain, 1978; Burla, Cascarano & Giacovazzo, 1992).
The option a) is the default, b) runs if the directive RANDOM is used. In this last case a large number (depending on the available computer time) of trials can be requested.
If a partial structure is available (the directive PARTIAL should have been used in the normalization routine) the PHASE routine is automatically able to take that information into account. No further directives are strictly necessary. However directives SYMBOLS, SPECIALS, MAXTRIAL may be used to change default values.
Phase expansion and refinement are carried out by means of a tangent formula using triplets, negative quartets, psi-zero triplets and the most reliable two-phase structure seminvariants. In the weighting scheme the experimental distributions of the alpha parameters are forced to match with the theoretical ones (Burla, Cascarano, Giacovazzo, Nunzi & Polidori, 1987).
For each phase set, several FOM's are computed using all invariants and seminvariants estimated by means of the representation method. Their meaning and an optimized way of combining all the computed FOM's to give a highly selective combined figure of merit (CFOM) is described in the papers by
Cascarano, Giacovazzo & Viterbo (1987) and by Cascarano, Giacovazzo & Guagliardi (1992).
All FOM's, as well as the combined CFOM, are expected to be equal to 1.0 for correct solutions. CFOM larger than 0.5 can be considered encouraging.
If pseudotranslational symmetry is present then CFOM > 0.3 may characterize the correct solution.
Several additional features have been introduced in the present version.
a) From the solution with the highest CFOM value a Fourier map may be calculated by involving a supplemental number of reflections which are expanded using the tangent formula (Altomare, Cascarano, Giacovazzo & Viterbo, 1991)
b) Special positions are handled, peaks very close to symmetry elements are moved onto symmetry elements, the site symmetry is defined and the atomic occupancy factor is calculated; key numbers for designating free, coupled or fixed positional parameters for least-squares subroutines are also calculated together with symmetry conditions on the thermal ellipsoid.
c) The set of peaks provided by the peak search routine is automatically analyzed in order to provide sound molecular fragments. If (as usually) the atomic species present in the unit cell are known, their atomic radii and (eventually) their chemical coordination are used in order to automatically identify fragments and relate peaks to the atomic species (automatic labelling of peaks). The above information is automatically processed via least-squares Fourier cycles in order to complete the crystal structure, reject false peaks and refine structural parameters (Altomare, Cascarano, Giacovazzo & Guagliardi, 1993). An isotropic diagonal matrix refinement is used ( if X-Ray radiation is used it does not involve H atoms). The final R's usually vary from 0.08 to 0.15.
SEARCH OF THE CORRECT SOLUTION
If SIR97 is not able to assign phases to reflections it will automatically increase the number of symbols in PHASE procedure and will restart it ; if the problem still remains, the program will use the RANDOM approach and after the MIXED approach.
If at the end of the automatic Fourier/Least-Squares procedure for the set no. 1 the residual value R is less then 25%, then the program assumes that a correct solution has not been found. It will automatically examine next solutions. When sets are exausted, the program will restart the PHASE procedure using a larger number of magic integers. Again the above procedure is repeated. If the correct solution is not found, the RANDOM and the MIXED approaches are used.
If a graphic interface is available, it is possible to interact with the model in order to complete and refine it.
The graphic interface incorporates a On-Line Help in order to describe al the features and tools available via graphics.
Thanks are due to T. Pilati and M. Moret for their routine integrated in SIR97 ( Polyhedra representation and electron density map contouring respectively ).
Species Serial_number x y z Thermal_factor Occupation
where the Thermal_factor is B(iso) for an isotropic atom (the exponential factor takes the form
exp[-B(sin()/)2] and the Thermal_factors are (11 12 13 22 23 33 ) for
an anisotropic atom (the exponential factor takes the form
![]()
The structure factors Fobs are used in the least squares refinement process and it is possible to ignore data with Fobs less than chop_value multiply (Fobs).
A variety of weighting schemes is available and the user can choose a scheme which does not give marked systematic trends with the magnitude of Fobs or of resolution. If the Cruickshank weighting scheme is selected, at the end of the refinement process a routine calculates the best coefficients of the function. In this way, the scheme would give constant <w2> when the set of w2 values is analysed in any significant systematic fashion and a value of the Goodness of Fit equal to the unit.
A damping factor can be set by the user to improve the convergence properties of the refinement.
The atomic parameters are refined using various type of matrix to accumulate the least squares derivatives. It is possible to use any user-defined blocks approximation starting from the full matrix type until the block diagonal per atom (4x4 for isotropic atom and 9x9 for anisotropic atom).
The scale factor is also refined and the constraints due to the space group are automatically taken into account. Nevertheless, the user can fix any parameters and set any equivalence between refined parameters.
If hydrogen atoms are present, their positional coordinates ride on the atoms to which they are attached and their isotropic thermal parameters are fixed equal to that of the attached atom.
SIR97 recognizes the following commands:
%INITIALIZE Initialize the direct access file (to override previous results and data)
%DATA Data input routine
%NORMAL Normalization routine
%SEMINVARIANTS Seminvariants routine
%INVARIANTS Invariants routine
%PHASE Converge-tangent routine
%FOURIER Automatic Fourier/Least-Squares routine
%MENU Access to graphical interface
%END End of the input file
%PATTERSON Patterson routine
%LSQ Least Squares routine
%GEOMETRY Geometrial calculation routine
%JOB A caption is printed in the output
%CONTINUE The program runs in default conditions from the last given command up to the end
%STRUCTURE string This command is used to specify the name of the structure to investigate. The program creates the name of the files needed adding the appropriate extension to the structure name. The file names are:
string.bin -> direct access file
string.ins -> final coordinates file
string.plt -> file for graphics
If this command is not used the default string "STRUCT" (instead of the name of the structure) is used to create file names.
%WINDOW [ x y ] Graphic window is required. Optionally it is possible to increase the dimension using x and y. Default values are 720, 525.
%NOWINDOW Graphic window is suppressed
Directives are described below, in the sections dedicated to the various routines.
All commands and directives are in free format (between columns 1-80) and are case independent. Only the first four characters are significant. The keywords can start in any position. If the first non-blank character is ">", then the record is interpreted as a comment.
SIR97 preserves intermediate results. For example, if invariant estimates have been already obtained during a previous run SIR97, in a new run the commands %INVARIANTS can be omitted.
Commands can be given in any order, under the following conditions:
- first routine used must be DATA, if it has not been used in a previous run;
- INVARIANT and SEMINVARIANT routines have no meaning if diffraction moduli are not normalized;
- PHASE routine has no meaning if no triplets have been calculated;
- FOURIER routine cannot run before PHASE routine.
- PSEUDO and PARTIAL directives require their own normalization. If one renounces to use PSEUDO or PARTIAL information, SIR97 must be restarted from %DATA command.
The minimal information needed by SIR97 is constituted by (see Example 1):
- cell parameters
- cell content
- space group symbol
- reflections
- electrons (if electron diffraction data are used).
The following limitations hold for commands and directives:
- seminvariants cannot be requested if PSEUDO is on;
- if PARTIAL is on, PSEUDO and RANDOM cannot be used;
- the directive SYMBOLS is of no use if RANDOM is on;
- PARTIAL and GENER are not compatible;
- PATTERSON followed by continue is not permitted.
cell dimensions a, b, and c are in angstroms, and in degrees.
SPACEGROUP string
String is the symbol of the space group, according to International Tables (1974). Blanks are necessary among the terms constituting the space group symbol (see examples at the end of this manual).
SHIFT sx sy sz
Origin shift components if desired by the user. They must be integral multiples of 1/24
CONTENTS El1 n1 El2 n2 El3 n3 .........
Unit cell contents. Eli is the chemical symbol of atomic type i, ni is the corresponding number of atoms in the unit cell (to a maximum of 8 atomic types). For each chemical element up to Cf (Z=98) X-ray and electrons scattering factor constants are stored, together with information on the atomic number and weight, covalent and Van-der-Waals radii., etc. in a file (see notes on implementation).
SFAC El a1 b1 a2 b2 a3 b3 a4 b4 c
Scattering factors for species El. If more lines are necessary, use character = at the end of the line.
ANOMALOUS El1 Df1 Df2
Values of f' and f" for species El.
ELECTRONS
This directive specifies that electron diffraction data will be used.
RHOMAX x
Maximum value of (sin()/)2 accepted for reflections to be used. The default is that all the data are accepted.
FORMAT string
String is the run time format to read reflections. Default value for string is (3I4,2F8.2).
RECORD n
It specificies the number of reflections per record, when n>1.
GENER
Reflections not in data will be generated having (sin()/)2 value less than the maximum value of (sin()/)2 in input.
REFLECTIONS string [R1,1 R1,2 R1,3 R2,1 R2,2 R2,3 R3,1 R3,2 R3,3]
String is the name of the reflections file. Records have n reflections, each with h,k,l,Fobs, (F) where h,k,l are integer (less than 63). If the orientation matrix Ri,j is supplied, it is immediately applied to reflections and all calculations will be performed using the final orientation. The end of reflections is detected using one of the following:
- blank record.
- end of file.
Negative values of Fobs are allowed; negative values of (F) are forbidden.
NOSIGMA
To be used when (F) values are meaningless or not available.
FOSQUARE
Program expects h,k,l, F2, (F2).
WAVE string
This directive is used to supply the wavelength value used only as information in CIF file produced by the program. Possible values for string are : Cu, Mo or a numeric value. Default wavelength is Mo.
Number of active reflections with largest E-values (up to 1500) subject to a minimum value of E(obs)= 1.2.Default is computed by he program. If PSEUDO directive is on, the program tries to use all the E's down to 1.2.
NZRO n
Number of smallest E-values to calculate psi-zero triplets. The default is 1/3 of the strong reflections.
BFAC x
Temperature factor if the user wants to supply it. (The scale factor is assumed equal to 1).
PSEUDO n(1,1) n(2,1) n(3,1) n(4,1) n(1,2) . . . n(4,3)
If parameters are equal to zero, or omitted, the normalization routine performs statistics for the pseudotraslation effects and renormalizes the reflections on assuming the most probable pseudotranslation as prior information.
If user wants to supply a specific pseudotranlational symmetry, and this corresponds to a class given in Table 1 the n(1,1) can be set to the class number and the other values must be omitted.
If the pseudotranslation is more complex, it should be specified by up to 3 sets of 4 values n(i,j) so that
( n(1,j)*h + n(2,j)*k +n(3,j)*l = n(4,j)*m ) j=1,3
where m is an integer number.
PARTIAL file_name
To perform the procedure which aims at recovering the complete structure from a partial one. This instruction is followed by the name of the file which contains the list of atomic information (one per card) consisting of atomic type, x, y, z and optionally occupancy factor ( default 1.0). See Example 3 - 4. Please consider the directive FRAGMENT in the module FOURIER/LEAST-SQUARES for a different approach.
LIST [n]
To print all reflections with the largest value of E (strong reflections). If n is supplied only n reflections will be listed. Default value of n is 10.
The number of the strongest reflections to use for one-phase seminvariants search.
Default value = number of strongest reflections chosen by normalization routine (max 350).
LIST
Print the list of the strongest reflections to use for one-phase seminvariants search.
The number of strongest reflections for the sigma2 search.
Default = number computed by normalization routine.
GMIN x
Triplets with G < x are not actively used.
Default value x=0.6 (in any case x > 0.2 and it is activated only if the P10 formula is applied).
EMIN x
Minimum value for the normalized structure factors in the sigma2 search.
Default = minimum value of E for the strongest reflections selected by normalization routine.
COCHRAN
To use the P3 formula. (By default P10 formula is used).
NUMK n
The number of free-vectors used by P10 formula.
Default value is provided by SIR97 according to the structural complexity:
n = min ( natom/msym + 30, 70 )
where natom is the number of atoms in the cell and msym is the number of symmetry operators of the space group.
CORRECTION x
If a pseudotranslation procedure is on, a correction factor depending on x is applied to the probabilistic argument of weak-weak-weak triplets when they are present. The default value is calculated by the program.
x = -1 eliminates weak-weak-weak triplets,
x = 1 corresponds to the largest confidence in them.
NQUARTETS
To not calculate negative quartets (Default uses them).
The number of reflections at the top of the divergence map for which a list of the map is obtained. Default = no printout of the map.
SYMBOLS n
The number of permuted phases (max 12). Default = 5.
PHASE n(i) phi(i) wt(i)
Codes, phases and weights of reflections with known phase (max 200). If one card is not sufficient, the directive PHASE must be repeated in the other card(s).
TABLE
To print the table of alpha values (at the beginning of PHASE procedure).
MINFOM x n
x: the program automatically stops when a solution is found with CFOM > x . Default value = 1.00.
n: is the maximum number of phase sets (with the largest combined figure of merit - CFOM) to retain (default value = 10).
RANDOM n
To use random phases starting sets.
n: is the number of random phases. If n is omitted, it is equal to one half of the strong reflections.
SEED n
Random generation seed. n must be an integer large value and must be odd. (Default 6753).
MAXTRIALS
Maximum number of trials when random approach is used. (Default 100).
NNEG
To not actively use negative triplets in the phasing process (Default uses them).
NNGQ
To not actively use negative quartets in the phasing process (Default uses them).
NOPS
To not actively use psi-zero triplets in the phasing process (Default uses them).
MIXED
The magic integer approach is applied to the best random sets to enhance the chance of finding the correct phases
The serial number of the set from which to calculate the E-map. If `SET n' is not specified, the set with the highest combined figure of merit will be used, and then if FOURIER routine is re-run, the set with the next highest combined figure of merit will be used.
MAP
If MAP is specified, the E-map will be printed on the lineprinter. The printing of the E-map is rarely used. The output is in sections of constant y with x across the page and z running down it on a grid of about three points per angstrom. The maximum number of grid points across the page is 36 ( i.e. about 12 angstroms in length). If more are needed, a new page is started.
GRID x
The grid on which the Fourier-map is evaluated will have a spacing of approximately x angstroms. The default spacing is computed by the program (0.3 A).
LIMITS l1 l2 l3
The E-map will be printed from 0 to l1 along x, from 0 to l2 along y, from 0 to l3 along z. (This directive can be used only if associated to MAP directive).
PEAKS n
The number of peaks to be searched for in the map. The default is the number of peaks for which
sum (occ(i)*m) = 1.3 * n
where occ is the crystallographic site occupancy factor, m is the number of symmetry operators, n is the number of non-hydrogen atoms in the unit cell..
LAYX
This directive can be used only if MAP directive is given. The Fourier-map will be printed in section of constant x.
LAYY
This directive can be used only if MAP directive is given. The Fourier-map will be printed in section of constant y.
LAYZ
This directive can be used only if MAP directive is given. The Fourier-map will be printed in section of constant z.
RADIUS El x
The value x of the radius used to compute the connectivity is assigned to element El.
RECYCLE n
Used to stop the recycling procedure after cycle number n. If n is equal to zero only the E-map will be calculated.
FOMIN x
Minimum value of F(obs) (on absolute scale) to be used in the recycling procedure.
SIGMA x
Reflections with F(obs)/sigma(F) greater than x will be used in the recycling procedure.
DMIN x
Distances less then x between atoms will be printed.
DMAX x
Distances up to x between atoms will be printed.
FRAGMENT string
Used to supply a known fragment to be completed. String is the name of the file in which, for each atom, are stored. Element X Y Z B(iso)
In the following directives string is used to supply the output file name. If string is omitted the default file name will be used (i.e. structure_name.ins and structure_name.plt for refinement and graphics respectively).
SCHAKAL string
A file containing atom coordinates is created in SCHAKAL format. This is the default.
SHELX string
A file containing atom coordinates is created in SHELX format.
CRYSTALS string
A file containing atom coordinates is created in CRYSTALS format.
COMPLETE
A file containing complete information for CRYSTALS program is created.
XYZ string
A file containing atom coordinates is created in XYZ format (Cartesian coordinates).
E**2 (or E*E)
Coefficients to be used in the Patterson synthesis.
F**2 (or F*F)
Coefficients to be used in the Patterson synthesis.
E*F (or F*E)
Coefficients to be used in the Patterson synthesis.
1) no indication (all the atoms have to considered);
2) Species (all the atoms belonging to that species have to be considered)
3) Label (only that atom has to be considered)
4) Label1 until Label2 (the atoms in the list starting from Label1 until Label2 have to be considered)
A mixed way can be used. Examples:
c (only carbon atoms are indicated)
c o (carbon and oxygen atoms are indicated)
c(1) (only this atoms is indicated)
c(1) until c(5) (if c(2), c(3) and c(4) are present in the list between c(1) and c(5), all this
atoms are considered)
c(1) c(12) (only c(1) and c(12) are considered)
c(2) c(7) until c(15) (the atoms c(2) and c(7),c(8),c(9)...,c(15) are considered)
To indicate the parameters, the following codes are used:
nothing x y z and b[iso] for isotropic atom
x y z and ijfor anisotropic atom
x y z positional coordinates
x's to indicate all three coordinates x, y and z
b[iso] to indicate the isotropic thermal parameter
11 12 13 22 23 33 ij anisotropic thermal parameters
ij ii to indicate the off- and the diagonal thermal parameters
occ occupation
scale bm overall scale and the overall temperature factor
NUMBER n
The number of the first calculation for this run.
For each reflection the output of structure factor calculation is printed
VERBOSE n
n is code to determine the level of printing:
n=0 (default conditions), the values of R% , wR% , S and some other general statistics
n=1 the atomic parameters
n=2 details of the refinement
ANOMALOUS code
code = ON the anomalous coefficients are taken into account (default condition)
code = OFF no anomalous scattering factor is introduced.
CYCLES n
n is the number of requested cycles
CALCULATION
Only one structure factor calculation is performed
WEIGHTING type npar par1 par2 ...
type number of the weighting scheme requested (1 - 12)
npar number of parameters
par1 par2 ... npar parameters of the weighting scheme
The available weighting schemes and parameters, stored in the direct access file,
are the following :
1 w = Fo/p(1) if Fo p(1)
w = p(1)/Fo if Fo p(1)
default ; p(1)=4*Fo(min)
2 w = 1/(p(1)+p(2)*Fo+p(3)*Fo**2 +...+p(n+1)*Fo**n )-
default: p(1)= 2*Fo(min); p(2)=1.0; p(3)=2./Fo(max)
3 w = (sin()/)**p(1)
default: p(1)=1.0
4 w = (/sin())**p(1)
default: p(1)=1.0
5 w = 1/((Fo ))**2
6 w = p(1)
default ; p(1)=1.0
7 w = 1/(1.+((Fo-p(2))/p(1))**2 )
default: p(1)= Fo(max); p(2)=Fo(min)
8 w = 1.0 if Fo p(1)
w = p(1)/Fo if Fo p(1)
default ; p(1)=4*Fo(min)
9 w = (Fo)
10 w = 1.0/(Fo)
11 w = (sin()/)**p(1) / (p(2)+p(3)*Fo+p(4)*Fo**2+. .+p(n+2)*Fo**(n))
default: p(1)=1.0; p(2)= 2*Fo(min); p(3)=1.0; p(4)=2./Fo(max)
12 w = 1./( (Fo )**2+p(1)*P+p(2)*P**2)
where P=(Fo+2Fc)/3 (shelx scheme)
default: p(1)=2.*P(min); p(2)=2./P(max)
CUTOFF chop_value
To ignore data with Fo less than chop_value multiplied by (Fo).
DAMPING damp
The calculated shifts are multiplied by damp before being added to the parameters
SCALE
To refine the scale only.
ISO atoms
The thermal factors of the atoms here indicated have to be transformed into isotropic ones
ANISO atoms
The thermal factors of the atoms here indicated have to be transformed into anisotropic ones
The following directives define the type of matrix to accumulate the least squares derivatives (they must be given together). This information is stored in the direct access file for a next use. Two type of directives exist, type A and type B ; the first directive must be of type A and only the directive BLOCK can be repeated to start the user-defined blocks approximation.
Type A:
FULLMATRIX atoms params
The parameters of the indicated atoms are included in a full matrix (the scale factor is automatically included). In the default way, all the atoms are included.
DIAGONAL atoms params
The parameters of the indicated atoms are refined using diagonal matrix approximation, one block per atom ; an extra block is added for the scale factor and the overall temperature factor. In the default way, all the atoms are included.
BLOCK atoms params
The parameters of the indicated atoms are included in the same block. The directive BLOCK has to be repeated for each block.
DEFAULT FULL
DEFAULT DIAG
To reset the refinement conditions.
Type B:
PLUS atoms params
The parameters of the indicated atoms are added to those defined by the previous instruction of type A
FIXED atoms params
To fix the parameters of the indicated atoms.
EQUIVALENCE atom1 param1 atom2 param2
To equivalence parameters of the selected atom(s). If atom2 is omitted, param1 and param2 are referred to the atom1 . Using this instruction, param1 is constrained to param2 in the least squares process and only one parameter is refined . This may be due to symmetry or any other constraint process. The obtained shift, multiplied by proper factor1 and factor2 respectively (see next instruction), is applied to param1 and param2 . The default value for factor1 and factor2 is 1.00.
FACTOR atom param coef
To set the value of the factor coef which multiplies the shift of the parameter of the indicated atom.
RIDE atoms1 atoms2
Normally the atoms2 indicates hydrogen atoms and atoms1 one of the species carbon, oxygen, nitrogen and boron if they are present in the content of the cell. The hydrogen coordinates 'ride' on the atoms to which they are attached.
END
To end the directives input.
Examples :
...
default full
...
diag o c
ride c h
...
full br(1) until c(15) x's ij
fix br(1) z
ride c h
...
block first until last x's
block o c ij
plus scale
...
block o
block c
plus scale
ride c h
...
block o c
plus scale
equiv o x y
...
full
plus c(1) occ
equiv c(1) occ c(11) occ
weight c(11) occ -1.0
...
block c(1) until c(48) x's ij
plus h(1) until h(483) x's
plus scale
ride c(1) until c(48) h(1) until h(483)
block c(101) until c(148) x's ij
plus h(11) until h(1483) x's
ride c(101) until c(148) h(11) until h(1483)
...
diag br(1) until c(12)
ride c h
Species(Serial_number,(Sym,Npl,Tx,Ty,Tz))
where Species and Serial_number are the usual label of the atom; (Sym is the number of the symmetry operator of the space group and the leading sign minus informs that the centrosymmetric operator is requested; Npl is the number of the lattice operator (see table below); Tx, Ty and Tz are positive or negative numbers indicating a lattice translation along axis a, b and c respectively.
The requested atom list in the instructions follows the rules given in LSQ module.
Lattic no. of Npl = Npl = 2 Npl = 3 Npl = 4 e operators 1 P 1 0 0 0 I 2 0 0 1/2 1/2 0 1/2 R 3 0 0 1/3 2/3 2/3 1/3 0 2/3 1/3 F 4 0 0 0 1/2 1/2 0 1/2 1/2 0 1/2 1/2 0 A 2 0 0 0 1/2 0 1/2 B 2 0 0 1/2 0 0 1/2 C 2 0 0 1/2 1/2 0 0One or more of the three following instruction must precede each request of geometrical calculation.
ATOM atoms
The named atoms have to be considered
LINE atom1 atom2
The two atoms identify a straight line
PLANE label
The label identifies the plane calculated before in the same run.
The following instructions allow the geometrical calculation.
P3P label
A plane for three atoms is calculated.
PQM label
A least-squares mean plane is calculated. Deviations of the atoms from the plane are listed.
PNR label
The coefficients of the plane perpendicular to a line and passing through an atom are calculated
DIST dmin dmax
Distances are calculated for all the indicated atoms in the range dmin - dmax
ANGLE dmin dmax
Bond angles are calculated for all the indicated atoms having distances in the range dmin - dmax.
TOR
The atoms define a chain of at least four atoms. A list of torsion angles is generated for all torsion angles defined by this chain.
APP
The angle between two planes is calculated.
ARP
The angle between a line and a plane is calculated
ALL
The angle between two lines is calculated
DPA
Distances of atoms from a plane are listed.
DRA
Distances of atoms from a line are listed.
SAVE
The subsequent bond length and angle calculation is stored.
CIF
A Crystallographic Information File file 'structure_name.cif' is created containing the bond lengths and angles stored in memory in the self-defining STAR format.
TABLE nc ndev nfix
The tables of bond lengths and angles previously stored are printed, ready for publication.
nc number of columns (default=2)
ndev number of digits for esd (default=1)
nfix = 0 decimal digits depending on esd (default)
= 1 number (3) of decimal digits is fixed
END
To end the directives input.
Examples :
%geometry
atom all the atoms have to be considered
dist bond distances in the default range 0.2-1.7
atom all the atoms
angle angles between atoms in the default distance range 0.2-1.7
atom c(1)
atom c(2)
atom c(3)
atom c(4)
atom c(5)
atom c(6)
atom o(6) the sequence c(1), c(2),..,o(6) defines a chain
torsion torsion angles are computed
atom all the atoms are selected
pqm p1 l.s. mean plane labelled 'p1' is calculated
atom c(1) until c(5)
atom o(5) the atoms between c(1) and c(5) plus o(5) are selected
pqm p2 l.s. mean plane labelled 'p2'
plane p1
plane p2
app the angle between the planes 'p1'^'p2' is calculated
line o(1) c(1) the line through the atoms o(1) and c(1) is defined
plane p2
arp the angle between the line and the plane 'p2'
atom o(1)
plane p2
dpa the distance of o(1) from the plane 'p2' is computed
line o(1) c(1)
atom c(7)
dra the distance of c(7) from the line o(1)-c(1) is computed
atom c(1)
atom c(2)
atom o(5)
p3p p3 the plane 'p3' through c(1),c(2) and o(5) is computed
line o(1) c(1)
plane p3
arp the angle between the line o(1)-c(1) and the plane 'p3'
line o(1) c(1)
line o(1) c(7)
all the angle between lines o(1)-c(1) and o(1)-c(7) is computed
line o(1) c(1)
atom c(1)
pnr p4 the plane perpendicular to the line o(1)-c(1) and
passing through the atoms c(1) is computed
plane p4
plane p3
app angle between planes 'p4' and 'p3'
save the following distance and angle calculated are stored
atom br(1) until c(12) the atoms between br(1) and c(12) are selected
dist 0.2 2.2 distances in the range 0.2-2.2 are calculated
atom c(1) until h(10)
dist 0.1 1.1 distances in the range 0.1-1.1
atom br(1) until c(12)
angle 0.2 2.2 angles between atoms in the distance range 0.2-2.2
atom c(1) until h(10)
angle 0.1 1.1
table distance and angle tables are printed
end
%end
a) the value of NREF (number of reflections actively used in the phasing process) is fixed by SIR. For some special structures the ratio "number of active triplets/NREF" is too small (e.g., less than 10). Larger values of NREF may improve the phasing procedure.
b) a check for possible pseudotranslational symmetry is always made by SIR: if PSEUDO keyword is not activated, then the information is given but not used in the phasing process. If a pseudotranslational symmetry has been found by the normalization routine a new run of SIR may be started including the keyword PSEUDO.
c) because of a faulty data collection strategy, often weak reflections may not be included in diffraction data. This lack of information influences both the normalization process (scale and overall thermal factors are affected by systematic errors; the experimental E-distribution is often non-centric even when the crystal structure is centrosymmetric) and the estimation of invariants and seminvariants: in particular, a reduced number of negative triplets ( via P10 formula) and of negative quartets is calculated. Success in the structure solution may be obtained if weak reflections are also used.
d) high (or low) resolution reflections may occasionally play a too important role in the first steps of convergence and divergence process. Fixing a thermal factor lower (or larger) than that provided by the normalization routine may successful change convergence and divergence process.
e) the use of 1- and 2- phase seminvariants are not default choices (they require additional computing time and often they are not necessary for the success of SIR). If symmetry is rather high, several seminvariants can be reliably estimated: some of them will actively be used in phase expansion and refinement process, others will be used as figures of merit. Sometimes the additional estimation of one or few one-phase seminvariants is enough for solving crystal structures.
f) an alternative space group should be carefully considered.
The following example shows the maximum default use of SIR. Most of the structures can be solved in this way. Diffraction data are in the file bobby.hkl in format (3I4,2F8.2), one reflection per record.
%Data
Cell 9.626 9.626 9.626 90 90 90
SpaceGroup P 21 3
Content H 24 C 24 N 4 O 24 Na 4 Ca 4
Reflections bobby.hkl
%Continue
Example 2
User wants to use in the phasing process the pseudotranslational symmetry (eventually identified in a previous run). Diffraction data are in fegas.hkl file with format (2(3I4,F10.4,F1.0)), two per record. (F) values are not in input file.
%Structure fegas
%Initilalize
%Job FE2GA2S5 2H P63/mmc
%Data
CELL 3.651 3.651 29.745 90. 90. 120.
SPACE P 63/M M C
CONT Fe 4 Ga 4 S 10
REFLECTIONS fegas.hkl
NOSIGMA
RECORD 2
FORMAT (2(3I4,F10.4,F1.0))
%NORMAL
PSEUDO
%CONTINUE
Example 3
The following example shows how to run partial procedure after that a complete run of SIR has been performed.
%STRUCTURE cephal
%JOB PARTIAL PROCEDURE RUN
%Normal
Partial cephal.frg
> Note that invariants and eventually seminvariants need not to be recomputed
%PHASE
%CONTINUE
The file cephal.frg contains :
C .3824 .1494 .2856
C .4344 .1415 .1688
C .3675 .1102 .2789
C .3866 .1546 .5060
C .4153 .0957 .1638
C .4088 .1654 .1820
Example 4
The following example shows how to use the partial procedure when a molecular fragment is located from other sources ( i.e. Patterson method ).
%WINDOW
%STRUCTURE CEPHAL
%INIT
%JOB - CEPHALOTAXIN C 2 -
%DATA
CELL 22.840 8.150 19.540 90. 117.7 90.
Space C 2
Cont C 144 H 168 O 32 N 8
Reflections cephal.hkl
RECORD 3
FORMAT (3(3I3,F7.2,1.0))
NOSIGMA
%NORMAL
PARTIAL cepahl.pat
%CONTINUE
Example 5
In the following example the use of one and two-phase seminvariants is requested together with 7 symbols to permute in PHASE routine. It is assumed that SIR was already ran before (thus normalization and invariants are not needed).
%structure bobby
%Seminv
%Phase
Symb 7
%continue
Example 6
In the following example only the E-map of the set number 7 and the complete FOURIER/LEAST-SQUARES procedure for set number 9 are requested by the user.
%Window 850 800
%Structure bobby
%FOURIER
SET 7
Recycle 0
%FOURIER
Set 9
%continue
Example 7
The user wants only view and eventually modify the structure previously produced by FOURIER routine and create a complete input file for CRYSTALS named CEPHAL.QCK .
%Structure cephal
%Menu
Crystals cephal.qck
Complete
%End
Example 8
In this example random approach is used and the best 200 sets, over 2000 trials, of phases are retained in the direct access file. No Fourier is required.
%NOWINDOW
%STRUCTURE cephal
%PHASE
RANDOM
MAXTRIALS 2000
MINFOM 1.0 200
%END
Example 9
In the following example the user known a fragment and wants to complete it using FOURIER/LEAST-SQUARES procedure. The binary file "azet.bin" must exist.
%WINDOW
%STRUCUTRE azet
%Fourier
Fragment azet.frg
%CONTINUE
Coordinates are in the file "azet.frg" which contains
Cl .02944 .72012 .08865
Cl .23727 .78692 .30869
1) h+k+l= 1n 2) h= 2n 3) k= 2n
4) l= 2n 5) h+k+l= 2n 6) h+k= 2n
7) h+l= 2n 8) k+l= 2n 9) h= 3n
10) k= 3n 11) l= 3n 12) h+k= 3n
13) h+l= 3n 14) k+l= 3n 15) h+k+l= 3n
16) h+k+2l= 3n 17) h+2k+l= 3n 18) 2h+k+l= 3n
19) h+2k= 3n 20) h+2l= 3n 21) k+2l= 3n
22) l= 4n 23) k= 4n 24) h= 4n
25) h+k= 4n 26 h+l= 4n 27) k+l= 4n
28) h+k+l= 4n 29) 2h+2k+l= 4n 30) 2h+k+2l= 4n
31) h+2k+2l= 4n 32) 2h+k+l= 4n 33) h+2k+l= 4n
34) h+k+2l= 4n 35) h+2k= 4n 36) h+2l= 4n
37) k+2l= 4n 38) 2h +k= 4n 39) 2h+l= 4n
40) 2k+l= 4n 41) 3h+3k+l= 4n 42) 3h+k+3l= 4n
43) h+3k+3l= 4n 44) h+2k+3l= 4n 45) h+3k+2l= 4n
46) 3h+k+2l= 4n 47) h+3k= 4n 48) h+3l= 4n
49) k+3l= 4n 50) 3k+2l= 6n 51) 2k+3l= 6n
52) 2h+3k= 6n 53) 3h+2k= 6n 54) 3h+2l= 6n
55) 2h+3l= 6n 56) 2h+2k+3l= 6n 57) 3h+2k+3l= 6n
58) 3h+3k+2l= 6n 59) 4k+3l=12n 60) 4h+3l=12n
61) 4h+3k=12n 62) 3k+4l=12n 63) 3h+4k=12n
64) 3h+4l=12n
65) h = 2n & k = 2n
66) h = 2n & l = 2n
67) k = 2n & l = 2n
68) h = 2n & k+l = 2n
69) k = 2n & h+l = 2n
70) l = 2n & h+k = 2n
71) h+k = 2n & h+l = 2n
72) h= 2n & k= 2n & l= 2n
2 - Camalli M., Giacovazzo C. & Spagna R. (1985). Acta Cryst. A41, 605-613.
3 - Cascarano G., Giacovazzo C. & Guagliardi A. (1991). Acta Cryst. A47, 698-702.
4 - Cascarano G., Giacovazzo C. & Guagliardi A. (1992). Acta Cryst. A48, 859-865.
5 - Cascarano G., Giacovazzo C. & Luic' M. (1988-a). Acta Cryst. A44, 176-183.
6 - Cascarano G., Giacovazzo C. & Luic' M. (1988-b) . Acta Cryst. A44, 183-188
7 - Cascarano G., Giacovazzo C. & Viterbo D. (1987), Acta Cryst. A43, 22-29.
8 - Cascarano G., Giacovazzo C., Calabrese G., Burla M.C., Nunzi A., Polidori G. & Viterbo D. (1984), Z. Kristallogr., 167, 34-47.
9 - Cascarano G., Giacovazzo C., Camalli M., Spagna R., Burla M.C., Nunzi A. & Polidori G. (1984), Acta Cryst. A40, 278-283.
10 - Cascarano G., Giacovazzo C., Burla M.C., Nunzi A. & Polidori G. (1984), Acta Cryst. A40, 389-394.
11 - Cochran W.(1955), Acta Cryst. 8,.473-478.
12 - Fan Haifu, Yao Jia-Xing & Qian Jin-zi (1988), Acta Cryst. A44, 688-691.
13 - Germain G., Main P. & Woolfson M.M. (1970), Acta Cryst. B26, 274-285.
14 - Giacovazzo C. (1976), Acta Cryst. A32, 958-966.
15 - Giacovazzo C. (1977), Acta Cryst. A33, 933-944.
16 - Giacovazzo C. (1978), Acta Cryst. A34, 562-574.
17 - Giacovazzo C. (1979), Acta Cryst. A35, 757-764.
18 - Giacovazzo C. (1980), Acta Cryst. A36, 362-372.
19 - Giacovazzo C. (1983), Acta Cryst. A39, 685-692.
20 - Giacovazzo C., Burla M.C. & Cascarano G. (1992), Acta Cryst. A48, 901-906.
21 - Giacovazzo C., Spagna R., Vickovic I. & Viterbo D. (1979), Acta Cryst. A35, 401-412.
22 - Main P. (1977), Acta Cryst. A33, 750-757.
23 - Main P. (1978), Acta Cryst. A34, 31-38.
24 - Main P., Fiske S.J., Hull S.E., Lessinger L., Germain G., Declercq J.P. & Woolfson M.M. (1980) - MULTAN80, a system of computer programs for the automatic solution of crystal structures from x-ray diffraction data - Univ. of York, England.
25 - Ten Eick,L.F. (1977), Acta Cryst. A33, 486-492.
26 - White P.S. & Woolfson M.M. (1975), Acta Cryst. A31, 53-56
27 - Giacovazzo C. (1993), Z. Kristallogr., 206, 161-171.
28 - Cascarano G. & Giacovazzo C. (1995), Acta Cryst. A51, 820-825.
29 - Camalli M., Capitani D., Cascarano G., Cerrini S., Giacovazzo C., Spagna R. (1986), Sir Caos (Italian Patent No. 35403c/86).
30 - Altomare A., Cascarano G., Giacovazzo C. & Guagliardi A. (1993). J. Appl. Cryst. 26, 343-350.
31 - Altomare A., Cascarano G., Giacovazzo C. & Viterbo D.(1991). Acta Cryst. A47, 744-748.
32 - Baggio R., Woolfson M.M., Declerq J.P. & Germain G.(1978). Acta Cryst. A34, 883-892
33 - Burla M.C., Cascarano G., Fares E., Giacovazzo C., Polidori G.& Spagna R. (1989). Acta Cryst. A45, 781-786
34 - Burla M.C., Cascarano G. & Giacovazzo C. (1992).Acta Cryst. A48, 906-912.
35 - Burla M.C., Giacovazzo C. & Polidori G.(1987).Acta Cryst. A43, 797-802.
36 - Burla M.C., Giacovazzo C. & Polidori G.(1989).Acta Crysta. A45, 94-104.
37 - Burla M.C., Cascarano G., Giacovazzo C., Nunzi A. & Polidori G. (1987), Acta Cryst. A43, 370-374.
38 - Burla M.C., Nunzi A., Giacovazzo C. & Polidori G. (1981), Acta Cryst. A37, 677-684.
39 - Altomare A.., Cascarano G., Giacovazzo C., Guagliardi A.., Burla M.C., Polidori G., Camalli M. (1994) J. Appl. Cryst. 27, 435-435.