Using the formula for the structure factor we can show that a reflection F(h,k,l) and its 'opposite', F(-h,-k,-l) will have the same magnitude and opposite phases. Try to compute this for any arbitrary atom coordinate (x,y,z) and any h,k,l you wish to use. This is called Friedel's Law. Centrosymmetrically related reflections in a non centrosymmetric space group are Friedel pairs, provided they are not otherwise related by space group symmetry (i.e, centric reflections per se, see below).
In case of the presence of anomalous contributions, a mixing of sin and cos terms breaks the centrosymmetry and the magnitude are not identical for Friedel opposites. The phases are not centrosymmetric around 0 anymore. This effect is exploited in anomalous dispersion phasing techniques.
It may be useful to review the vector presentations of the structure factor to visualize this phenomenon. Notice also the special case of only anomalous scatterers (or one single anomalous atom), where only the phase symmetry is broken, but the magnitudes remain the same.
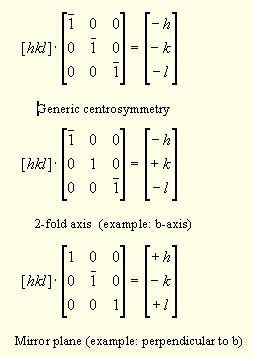
Centric reflections
Reflection pairs F(h,k,l) and F(-h,-k,-l) and that are related through the space group's point symmetry (Laue symmetry) are not Friedel pairs. They are called centric reflections and have in any case the same intensity. They can be used to determine data quality statistics (merging statistics) in the absence of anomalous contributions. A comparison of their statistics to the merged Friedel pairs, which should merge significantly higher, indicates whether a useable anomalous signal is present. Some examples for centric reflections generated by point group symmetry (see International Tables for more operators) :
Systematic absences of reflections due to space group symmetry
Plugging numbers into the structure factor formulas (or expanding the terms and reducing the mess) shows that the internal symmetry operations screws and glides (which include translational components) and the Bravais translations yield systematic absences in the diffraction pattern regardless of the cell content. We distinguish serial and zonal extinctions, cause by the presence of screws and glides, respectively, and integral extinctions caused by Bravais translation vectors. The international tables list the conditions for possible reflections for each space group. For example, a F centered lattice would have all 3 indices of a triple either even or odd, or a 2-fold screw axis parallel to c would show only even idices l in 0,0,l reflections .
The systematic absences allow to determine certain space groups unambiguously, but in many cases a unique determination of the space group by crystallographic means alone is not possible. Fortunately, there are a number of additional clues (number of molecules in cell, chirality of motif, physical properties) which allow to determine the space groups correctly. Try for example P 2 2 2 and P m m m. In case of a protein crystal you would know that P m m m is not a possible space group, because P m m m is centrosymmetric (check the output listing).

What is the symmetry operation causing the extinctions in the lattice on
the left? What are the possible space groups?
What causes the kind of extinctions observerd in the lattice on the right?
Click here to submit your answer. If your answer is right, you will be listed in the Space Group Hall of Fame. If not, I'll reply and explain. In case you worry, I will not list wrong answers, nor sue you for it, or make fun.
Non-crystallographic symmetry
Difficult cases for space group determination may be encountered where for example non-crystallographic symmetry (NCS) exists. A NCS 2-fold axis for example may be initially interpreted as crystallographic axis. The refinement in the higher symmetric spacegroup may not converge well and show high R-values, whereas the refinement of the (slightly different) 2 individual molecules in the lower symmetric space group yields better refinement and the correct structure. An evaluation of the statistic parameters including Rfree must justify this approach, however. If you are interested in NCS and the use of native Patterson maps to detect NCS, go to our antibody structure.
![]() Back to X-ray Tutorial Introduction
Back to X-ray Tutorial Introduction
LLNL Disclaimer
This World Wide Web site conceived and maintained by
Bernhard Rupp (br@llnl.gov)
Last revised June 26, 1998 10:06
UCRL-MI-125269